こんにちは、ふみです。みなさんは日常生活で連立方程式を使うことはありますか?
私は競馬の勝馬投票券(馬券)で複数の組み合わせを購入する際、どの組み合わせが当たっても同じような配当になるようにするため、組み合わせ毎の購入金額を連立方程式で計算することがあります。
連立方程式の計算で、どの組み合わせが当たっても同じような配当にすることができれば、トリガミ(当たっているのに損すること)をほぼなくすことができます。
連立方程式は表計算ソフト「Microsoft Excel(エクセル)」でも計算することができます。
CONTENTS
2元1次方程式
連立方程式は中学2年生で習います。
x と y を組み合わせた2つの式から x と y の数字を求めるのが2元1次方程式です。
馬券の買い方を2元1次方程式に当てはめる
ここでは競馬で馬券を購入する例を使って解説します。
どの組み合わせで当たっても同じ配当になる馬券の買い方は連立方程式で解くことができます。
同じレースに出走する単勝16倍の馬と単勝64倍の馬の2つの単勝馬券を購入するとき、単勝16倍の購入金額を x、単勝64倍の購入金額を y とします。
1レースの合計購入金額が1,000円で、どちらが勝っても同じ配当になるように購入する場合、連立方程式に当てはめると次のような2元1次方程式になります。
| x + y = 1000 16x = 64y |
2元1次方程式をExcelで計算する
2元1次方程式をExcelで計算するには行列の計算を使います。現在の高校数学では行列の計算を習わないようなので、少し丁寧に解説します。
Excelで行列の計算をするには2元1次方程式を「ax + by = 定数」の形にします。
| x + y = 1000 16x – 64y = 0 |
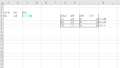
この2つの式をExcelシートに入力します。「ax + by」の a と b の値をセルB2~C3、「定数」の値をセルE2~E3に入力すると次のようになります。
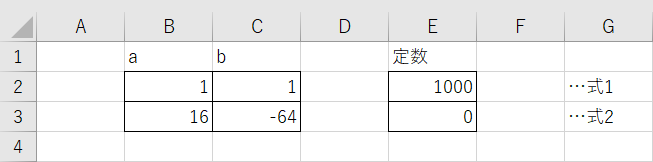
Excelではこのように行列のようにセルに並べて数値を置くと配列計算ができるようになります。
2つの式は行列の形に変形すると次のようになります。
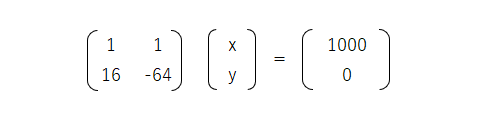
一番左の行列(セルB2~C3)をAとしたときに両辺の左側にA-1を掛ける※と左辺に単位行列ができます。つまりA-1(Aの逆行列)に一番右側の定数の行列(セルE2~E3)を掛けると x と y の解の行列を求めることができます。(※右側からA-1掛けると x と y の行列が間に挟まるので左辺に単位行列ができません。故にA-1は左側から掛けます。)
まずは配列関数の MINVERSE関数を使ってAの逆行列(A-1)を求めます。
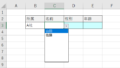
セルB5~C6を選択した状態で数式バーに次の式を入力します。
=MINVERSE($B$2:$C$3)
MINVERSE関数は数式を入力し、 Ctrl + Shift + Enter で配列数式として認識されます。(Office2019)
配列数式が機能すると数式バーに表示されている数式の両端に波カッコが表示され、セルB5~C6にセルB2~C3の逆行列(A-1)が表示されます。
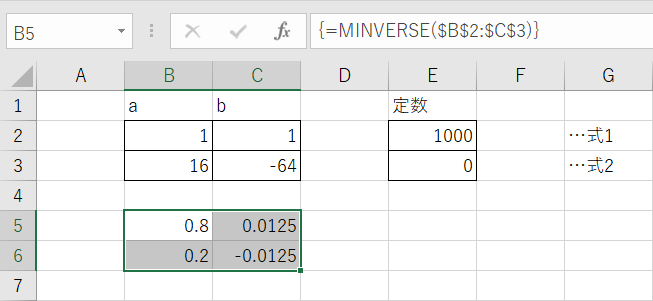
逆行列ができたらこの逆行列(セルB5~セルC6)に定数の行列(セルE2~E3)を掛けます。
現在の状態を行列の形で表すと次のようになります。

行列の掛け算は配列関数のMMULT関数を使います。
セルB8~B9を選択した状態で数式バーに次の式を入力します。
=MMULT($B$5:$C$6,$E$2:$E$3)
MMULT関数は数式を入力し、Ctrl + Shift + Enter で入力すると配列数式として認識されます。(Office2019)
配列数式が機能すると数式バーに表示されている数式の両端に波カッコが表示され、セルB8~B9に連立方程式の解の行列が表示されます。
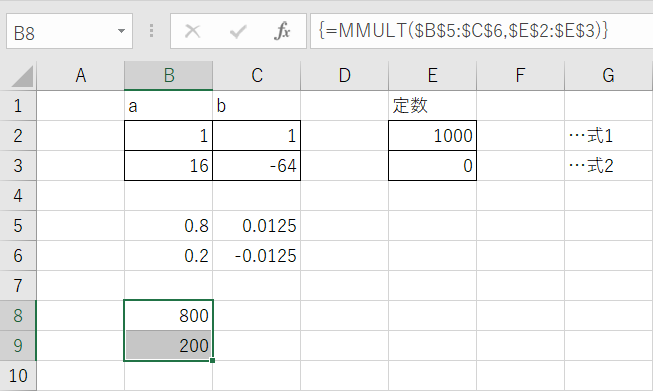
これで連立方程式の解 x = 800、y = 200 が表示されました。
連立方程式の解のとおり、単勝16倍の馬を800円、単勝64倍の馬を200円購入すると、合計金額は 800 + 200 = 1,000(円)で、単勝16倍の馬が勝った時の配当は 800 × 16 = 12,800(円)、単勝64倍の馬が勝った時の配当も 200 × 64 = 12,800(円)となるので、どちらが勝っても同じ配当になります。
2元1次方程式をExcelで検算する
連立方程式が正しく解けていれば、行列Aに連立方程式の解の行列を掛けると定数の行列になります。検算を行列の形に変形すると次のようになります。
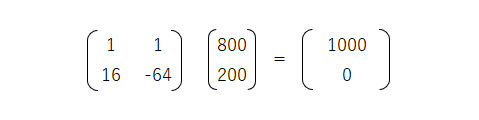
行列の掛け算なので、配列関数のMMULT関数を使います。
セルB11~B12を選択した状態で数式バーに次の式を入力します。
=MMULT($B$2:$C$3,$B$8:$B$9)
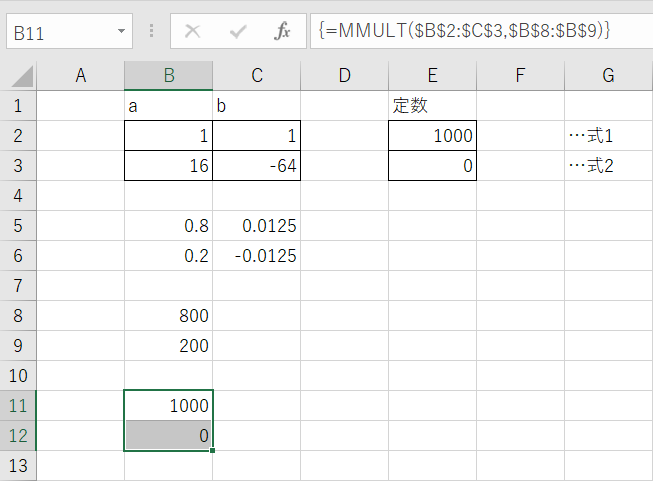
MMULT関数は数式を入力し、Ctrl + Shift + Enter で入力すると配列数式として認識されます。(Office2019)
配列数式が機能すると数式バーに表示されている数式の両端に波カッコが表示されます。
セルB11~B12に定数の行列(セルE2~E3)の値が表示されれば、連立方程式が正しく解けています。
3元1次方程式
x と y と z を組み合わせた3つの式から x と y と z の数字を求めるのが3元1次方程式です。
馬券の買い方を3元1次方程式に当てはめる
ここでも競馬で馬券を購入する例を使って解説します。
どの組み合わせで当たっても同じ配当になる馬券の買い方は連立方程式で解くことができます。
同じレースに出走する単勝1.6倍の馬と単勝3.2倍と単勝9.6倍の馬の3つの単勝馬券を購入するとき、単勝1.6倍の購入金額を x、単勝3.2倍の購入金額を y 、単勝9.6倍の購入金額を z とします。
1レースの合計購入金額が2,000円で、どの馬が勝っても同じ配当になるように購入する場合、連立方程式に当てはめると次のような3元1次方程式になります。
| x + y + z = 2000 1.6x = 3.2y 1.6x = 9.6z |
3元1次方程式をExcelで計算する
3元1次方程式をExcelで計算するには行列の計算を使います。
Excelで行列の計算をするには3元1次方程式を「ax + by + cz = 定数」の形にします。
| x + y + z = 2000 1.6x – 3.2y = 0 1.6x – 9.6z = 0 |
この3つの式をExcelシートに入力します。「ax + by + cz」のaとbとcの値をセルB2~D4、「定数」の値をセルF2~F4に入力すると次のようになります。
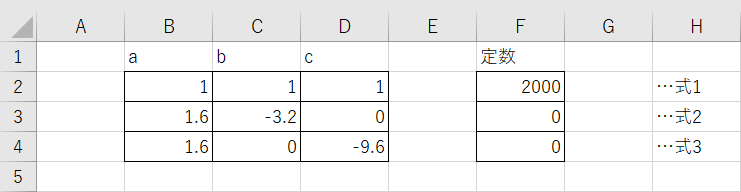
3つの式は行列の形に変形すると次のようになります。
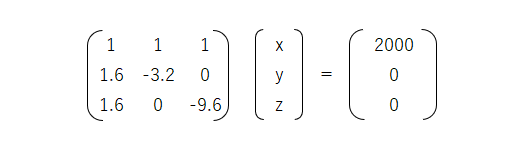
一番左の行列(セルB2~D4)をAとしたときに両辺の左側にA-1を掛けると左辺に単位行列ができます。つまりA-1(Aの逆行列)に一番右側の定数の行列(セルF2~F4)を掛けると x、y、z の解の行列を求めることができます。
まずは配列関数の MINVERSE関数を使ってAの逆行列(A-1)を求めます。
セルB6~D8を選択した状態で数式バーに次の式を入力します。
=MINVERSE($B$2:$D$4)
MINVERSE関数は数式を入力し、 Ctrl + Shift + Enter で配列数式として認識されます。(Office2019)
配列数式が機能すると数式バーに表示されている数式の両端に波カッコが表示され、セルB6~D8にセルB2~D4の逆行列(A-1)が表示されます。
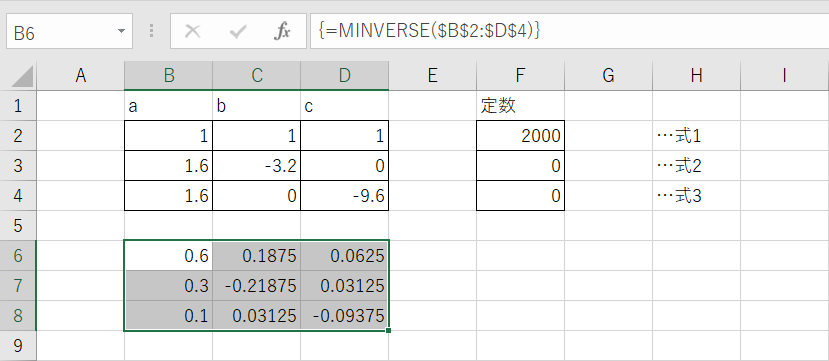
逆行列ができたらこの逆行列(セルB6~セルD8)に定数の行列(セルF2~F4)を掛けます。
現在の状態を行列の形で表すと次のようになります。

行列の掛け算は配列関数の MMULT関数を使います。
セルB10~B12を選択した状態で数式バーに次の式を入力します。
=MMULT($B$6:$D$8,$F$2:$F$4)
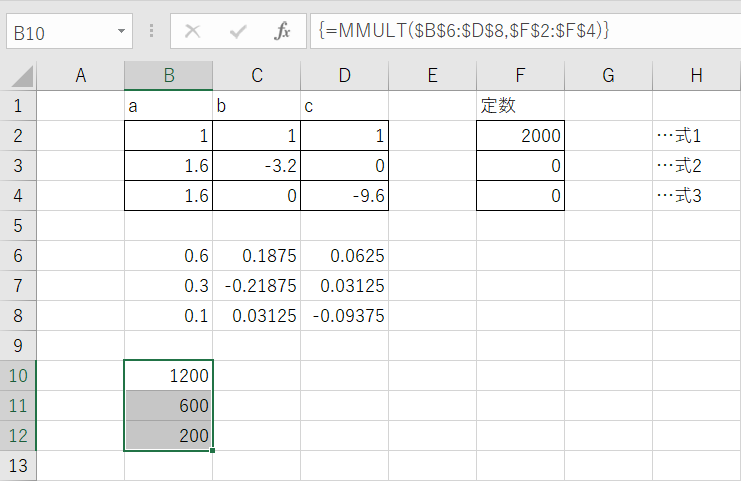
これで連立方程式の解 x = 1,200、y = 600、z = 200 が表示されました。
連立方程式の解のとおり、単勝1.6倍の馬を1,200円、単勝3.2倍の馬を600円、単勝9.6倍の馬を200円購入すると、合計金額は 1,200 + 600 + 200 = 2,000(円)で、単勝1.6倍の馬が勝った時の配当は 1,200 × 1.6 = 1,920(円)、単勝3.2倍の馬が勝った時の配当も 600 × 3.2= 1,920(円)、単勝9.6倍の馬が勝った時の配当も 200 × 9.6 = 1,920(円)となるので、どの馬が勝っても同じ配当になります。
そして、どの馬が勝ってもトリガミ(当たっているのに損すること)になることから、このレースでは単勝馬券を買わない方が良いことが分かります。
3元1次方程式をExcelで検算する
連立方程式が正しく解けていれば、行列Aに連立方程式の解の行列を掛けると定数の行列になります。検算を行列の形に変形すると次のようになります。
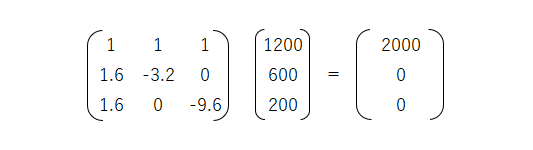
行列の掛け算なので、配列関数の MMULT関数を使います。
セルB14~B16を選択した状態で数式バーに次の式を入力します。
=MMULT($B$2:$D$4,$B$10:$B$12)
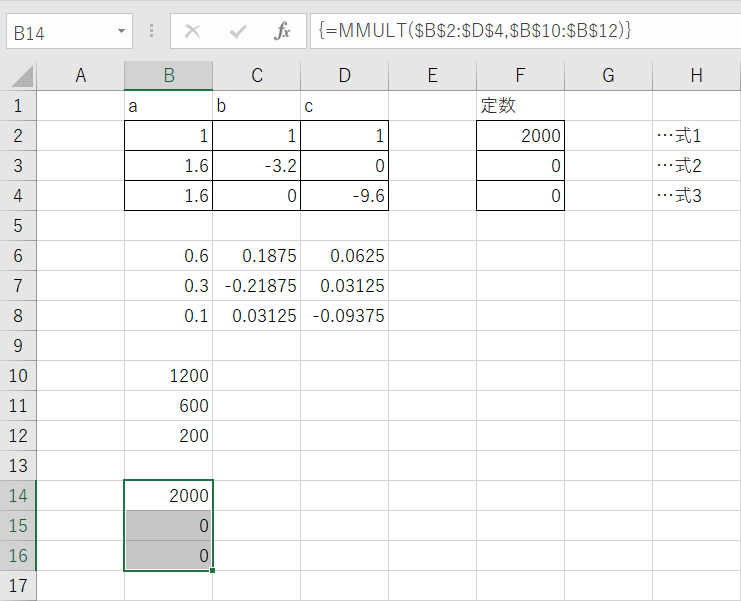
MMULT関数は数式を入力し、Ctrl + Shift + Enter で入力すると配列数式として認識されます。(Office2019)
配列数式が機能すると数式バーに表示されている数式の両端に波カッコが表示されます。
セルB14~B16に定数の行列(セルF2~F4)の値が表示されれば、連立方程式が正しく解けています。
行列の用語解説
行列の計算を学校で習わなかった(理解できなかった)人でも、単位行列と逆行列の性質だけ理解しておけば、Excelで連立方程式を解く仕組みがわかりやすくなると思います。
単位行列
左上から右下への対角成分に 1 が並び、他は全て 0 となる行列を単位行列といいます。
単位行列をEとした時、行列Aと掛け算をすると
| AE = EA = A |
が成立します。
単位行列は整数の掛け算における「1」のような性質をもつ行列です。
ちなみに、単位行列をスカラー倍したものをスカラー行列といいます。
逆行列
単位行列をEとした時、行列Aと行列Bの計算で
| AB = E = BA |
が成立するとき、行列BはAの逆行列といい、A-1と表します。
逆行列は整数の掛け算における、逆数のような性質をもつ行列です。
まとめ
- 連立方程式は行列の計算で解くことができる
- 逆行列の計算は配列関数の MINVERSE関数を使う
- 行列の掛け算は配列関数の MMULT関数を使う
- 配列関数を含む数式は Ctrl + Shift + Enter で入力すると配列数式として認識される
- 単位行列は整数の掛け算における「1」のような性質をもつ行列
- 逆行列は整数の掛け算における、逆数のような性質をもつ行列
ありがとうございました。
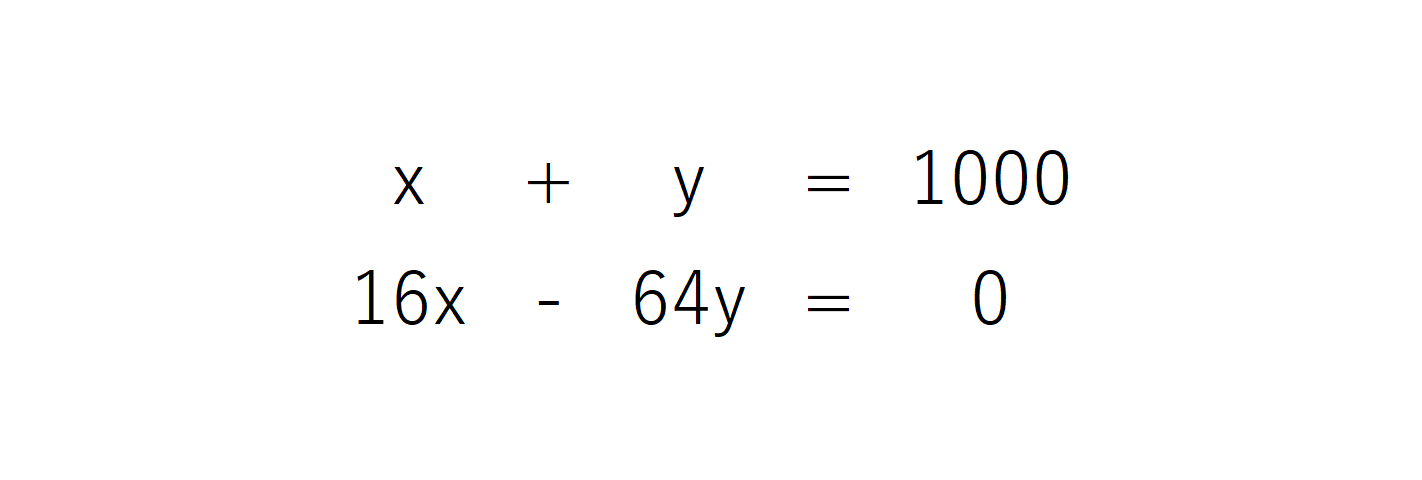
コメント